In mathematics, a series is often represented as the sum of a sequence of terms. That is, a series is represented as a list of numbers with addition operations between them, for example this arithmetic sequence:
1 + 2 + 3 + 4 + 5 + ... + 99 + 100.
In most cases of interest the terms of the sequence are produced according to a certain rule, such as by a formula, by an algorithm, by a sequence of measurements, or even by a random number generator.
A series may be finite or infinite. Finite series may be handled with elementary algebra, but infinite series require tools from mathematical analysis if they are to be applied in anything more than a tentative way.
Examples of simple series include the arithmetic series which is a sum of an arithmetic progression, written as:

and finite geometric series, a sum of a geometric progression, which can be written as:


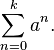
Infinite series
Mathematicians usually study a series as a pair of sequences: the sequence of terms of the series: a₀, a₁, a₂, … and the sequence of partial sums S₀, S₁, S₂, …, where S_n = a₀ + a₁ + … + a_n. The notation

represents then a priori this pair of sequences, which is always well defined, but which may or may not converge. In the case of convergence, i.e., if the sequence of partial sums S_N has a limit, the notation is also used to denote the limit of this sequence. To make a distinction between these two completely different objects (sequence vs. numerical value), one may sometimes omit the limits (atop and below the sum's symbol) in the former case, although it is usually clear from the context which one is meant.
Also, different notions of convergence of such a sequence do exist (absolute convergence, summability, etc). In case the elements of the sequence (and thus of the series) are not simple numbers, but, for example, functions, still more types of convergence can be considered (pointwise convergence, uniform convergence, etc.; see below).
Mathematicians extend this idiom to other, equivalent notions of series. For instance, when we talk about a recurring decimal, we are talking, in fact, just about the series for which it stands (0.1 + 0.01 + 0.001 + …). But because these series always converge to real numbers (because of what is called the completeness property of the real numbers), to talk about the series in this way is the same as to talk about the numbers for which they stand. In particular, it should offend no sensibilities if we make no distinction between 0.111… and /₉. Less clear is the argument that 9 × 0.111… = 0.999… = 1, but it is not untenable when we consider that we can formalize the proof knowing only that limit laws preserve the arithmetic operations. See 0.999... for more.

History of the theory of infinite series
The idea of an infinite series expansion of a function was first conceived in India by Madhava in the 14th century, who also developed the concepts of the power series, the Taylor series, the Maclaurin series, rational approximations of infinite series, and infinite continued fractions. He discovered a number of infinite series, including the Taylor series of the trigonometric functions of sine, cosine, tangent and arctangent, the Taylor series approximations of the sine and cosine functions, and the power series of the radius, diameter, circumference, angle θ, π and π/4. His students and followers in the Kerala School further expanded his works with various other series expansions and approximations, until the 16th century.
In the 17th century, James Gregory also worked on infinite series and published several Maclaurin series. In 1715, a general method for constructing the Taylor series for all functions for which they exist was provided by Brook Taylor. Leonhard Euler in the 18th century, developed the theory of hypergeometric series and q-series.

Development of infinite series
The study of the convergence criteria of a series began with Madhava in the 14th century, who developed tests of convergence of infinite series, which his followers further developed at the Kerala School.
In Europe however, the investigation of the validity of infinite series is considered to begin with Gauss in the 19th century. Euler had already considered the hypergeometric series

on which Gauss published a memoir in 1812. It established simpler criteria of convergence, and the questions of remainders and the range of convergence.
Cauchy (1821) insisted on strict tests of convergence; he showed that if two series are convergent their product is not necessarily so, and with him begins the discovery of effective criteria. The terms convergence and divergence had been introduced long before by Gregory (1668). Leonhard Euler and Gauss had given various criteria, and Colin Maclaurin had anticipated some of Cauchy's discoveries. Cauchy advanced the theory of power series by his expansion of a complex function in such a form.
Abel (1826) in his memoir on the binomial series

corrected certain of Cauchy's conclusions, and gave a completely scientific summation of the series for complex values of m and x. He showed the necessity of considering the subject of continuity in questions of convergence.
Cauchy's methods led to special rather than general criteria, and the same may be said of Raabe (1832), who made the first elaborate investigation of the subject, of De Morgan (from 1842), whose logarithmic test DuBois-Reymond (1873) and Pringsheim (1889) have shown to fail within a certain region; of Bertrand (1842), Bonnet (1843), Malmsten (1846, 1847, the latter without integration); Stokes (1847), Paucker (1852), Tchebichef (1852), and Arndt (1853).
General criteria began with Kummer (1835), and have been studied by Eisenstein (1847), Weierstrass in his various contributions to the theory of functions, Dini (1867), DuBois-Reymond (1873), and many others. Pringsheim's (from 1889) memoirs present the most complete general theory.

Convergence criteria
The theory of uniform convergence was treated by Cauchy (1821), his limitations being pointed out by Abel, but the first to attack it successfully were Seidel and Stokes (1847-48). Cauchy took up the problem again (1853), acknowledging Abel's criticism, and reaching the same conclusions which Stokes had already found. Thomae used the doctrine (1866), but there was great delay in recognizing the importance of distinguishing between uniform and non-uniform convergence, in spite of the demands of the theory of functions.

Uniform convergence
A series is said to be semi-convergent (or conditionally convergent) if it is convergent but not absolutely convergent.
Semi-convergent series were studied by Poisson (1823), who also gave a general form for the remainder of the Maclaurin formula. The most important solution of the problem is due, however, to Jacobi (1834), who attacked the question of the remainder from a different standpoint and reached a different formula. This expression was also worked out, and another one given, by Malmsten (1847). Schlömilch (Zeitschrift, Vol.I, p. 192, 1856) also improved Jacobi's remainder, and showed the relation between the remainder and Bernoulli's function

Genocchi (1852) has further contributed to the theory.
Among the early writers was Wronski, whose "loi suprême" (1815) was hardly recognized until Cayley (1873) brought it into prominence.

Semi-convergence
Fourier series were being investigated as the result of physical considerations at the same time that Gauss, Abel, and Cauchy were working out the theory of infinite series. Series for the expansion of sines and cosines, of multiple arcs in powers of the sine and cosine of the arc had been treated by Jakob Bernoulli (1702) and his brother Johann Bernoulli (1701) and still earlier by Viète. Euler and Lagrange simplified the subject, as did Poinsot, Schröter, Glaisher, and Kummer.
Fourier (1807) set for himself a different problem, to expand a given function of x in terms of the sines or cosines of multiples of x, a problem which he embodied in his Théorie analytique de la Chaleur (1822). Euler had already given the formulas for determining the coefficients in the series; Fourier was the first to assert and attempt to prove the general theorem. Poisson (1820-23) also attacked the problem from a different standpoint. Fourier did not, however, settle the question of convergence of his series, a matter left for Cauchy (1826) to attempt and for Dirichlet (1829) to handle in a thoroughly scientific manner (see convergence of Fourier series). Dirichlet's treatment (Crelle, 1829), of trigonometric series was the subject of criticism and improvement by Riemann (1854), Heine, Lipschitz, Schläfli, and DuBois-Reymond. Among other prominent contributors to the theory of trigonometric and Fourier series were Dini, Hermite, Halphen, Krause, Byerly and Appell.

Fourier series

In general, the geometric series

converges if and only if |z| < 1.

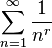
converges if r > 1 and diverges for r ≤ 1, which can be shown with the integral criterion described below in convergence tests. As a function of r, the sum of this series is Riemann's zeta function.

converges if the sequence b_n converges to a limit L as n goes to infinity. The value of the series is then b₁ − L.

A geometric series is one where each successive term is produced by multiplying the previous term by a constant number. Example:
The harmonic series is the series
An alternating series is a series where terms alternate signs. Example:
The series
A telescoping series Some types of infinite series
Main article: absolute convergence.
A series

is said to converge absolutely if the series of absolute values

converges. In this case, the original series, and all reorderings of it, converge, and converge towards the same sum.
The Riemann series theorem says that if a series converges, but not absolutely, then one can always find a reordering of the terms so that the reordered series diverges. Moreover, if the a_n are real and S is any real number, one can find a reordering so that the reordered series converges with limit S.

Absolute convergence

Main article: convergence tests Convergence tests
Several important functions can be represented as Taylor series; these are infinite series involving powers of the independent variable and are also called power series. For example, the series

converges to e for all x. See also radius of convergence.
Historically, mathematicians such as Leonhard Euler operated liberally with infinite series, even if they were not convergent. When calculus was put on a sound and correct foundation in the nineteenth century, rigorous proofs of the convergence of series were always required. However, the formal operation with non-convergent series has been retained in rings of formal power series which are studied in abstract algebra. Formal power series are also used in combinatorics to describe and study sequences that are otherwise difficult to handle; this is the method of generating functions.

Power series

Main article: Dirichlet series Dirichlet series
Asymptotic series, otherwise asymptotic expansions, are infinite series whose partial sums become good approximations in the limit of some point of the domain. In general they do not converge. But they are useful as sequences of approximations, each of which provides a value close to the desired answer for a finite number of terms. The difference is that an asymptotic series cannot be made to produce an answer as exact as desired, the way that convergent series can. In fact, after a certain number of terms, a typical asymptotic series reaches its best approximation; if more terms are included, most such series will produce worse answers.
Cesàro summation, (C,k) summation, Abel summation, and Borel summation provide increasingly weaker (and hence applicable to increasingly divergent series) means of defining the sums of series.
The notion of series can be defined in every abelian topological group; the most commonly encountered case is that of series in a Banach space.

Generalizations
Analogous definitions may be given for sums over arbitrary index set. Let a: I → X, where I is any set and X is an abelian topological group. Let F be the collection of all finite subsets of I. Note that F is a directed set ordered under inclusion with union as join. We define the sum of the series as the limit

if it exists and say that the series a converges unconditionally. Thus it is the limit of all finite partial sums. Because F is not totally ordered, and because there may be uncountably many finite partial sums, this is not a limit of a sequence of partial sums, but rather of a net.
Note, however that needs to be countable for the sum to be finite. To see this, suppose it is uncountable. Then some would be uncountable, and we can estimate the sum

This definition is insensitive to the order of the summation, so the limit will not exist for conditionally convergent series. If, however, I is a well-ordered set (for example any ordinal), one may consider the limit of partial sums of the finite initial segments

If this limit exists, then the series converges. Unconditional convergence implies convergence, but not conversely, as in the case of real sequences. If X is a Banach space and I is well-ordered, then one may define the notion of absolute convergence. A series converges absolutely if

exists. If a sequence converges absolutely then it converges unconditionally, but the converse only holds in finite dimensional Banach spaces.
Note that in some cases if the series is valued in a space that is not separable, one should consider limits of nets of partial sums over subsets of I which are not finite.

Summations over arbitrary index sets
For real-valued series, an uncountable sum converges only if at most countably many terms are nonzero. Indeed, let

be the set of indices whose terms are greater than 1/n. Each I_n is finite (otherwise the series would diverge). The set of indices whose terms are nonzero is the union of the I_n by the Archimedean principle, and the union of countably many countable sets is countable by the axiom of choice.
Occasionally integrals of real functions are described as sums over the reals. The above result shows that this interpretation should not be taken too literally. On the other hand, any sum over the reals can be understood as an integral with respect to the counting measure, which accounts for the many similarities between the two constructions.
The proof goes forward in general first-countable topological vector spaces as well, such as Banach spaces; define I_n to be those indices whose terms are outside the n-th neighborhood of 0. Thus uncountable series can only be interesting if they are valued in spaces that are not first-countable.

Examples

Convergent series
Divergent series
Sequence transformations
Sequence