Heat engines
The second law of thermodynamics puts a fundamental limit on the thermal efficiency of heat engines. Surprisingly, even an ideal, frictionless engine can't convert anywhere near 100% of its input heat into work. The limiting factors are the temperature at which the heat enters the engine, 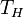, and the temperature of the environment into which the engine exhausts its waste heat,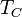, measured in the absolute Kelvin or Rankine scale. From Carnot's theorem, for any engine working between these two temperatures:

This limiting value is called the Carnot cycle efficiency because it is the efficiency of an unattainable, ideal, lossless (reversible) engine cycle called the Carnot cycle. No heat engine, regardless of its construction, can exceed this efficiency.
Examples of 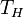are the temperature of hot steam entering the turbine of a steam power plant, or the temperature at which the fuel burns in an internal combustion engine. 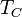is usually the ambient temperature where the engine is located, or the temperature of a lake or river that waste heat is discharged into. For example, if an automobile engine burns gasoline at a temperature of and the ambient temperature is , then its maximum possible efficiency is given by: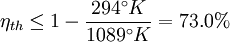

In practice, because no practical implementation of the Carnot cycle exists coupled with other irreversibilities such as the combustion process itself and friction, real engines fall far short of the Carnot efficiency. Real automobile engines are only around 25% efficient, combined cycle power stations have efficiencies much higher however will still fall at least 15% points short of the Carnot value. As Carnot's theorem only applies to heat engines, devices that convert the fuel's energy directly into work without burning it such as fuel cells, can exceed the Carnot efficiency.

Carnot efficiency
For an energy conversion device like a boiler or furnace, the thermal efficiency is . So, for a boiler that produces 210 kW (or 700,000 BTU/h) output for each 300 kW (or 1,000,000 BTU/h) heat-equivalent input, its thermal efficiency is 210/300 = 0.70, or 70%. This means that the 30% of the energy is lost to the environment.
An electric resistance heater has a thermal efficiency of at or very near 100%, so, for example, 1500W of heat are produced for 1500W of electrical input. When comparing heating units, such as a 100% efficient electric resistance heater to an 80% efficient natural gas-fueled furnace, an economic analysis is needed to determine the most cost-effective choice.

Energy conversion
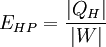
Heat pumps, refrigerators, and air conditioners, for example, move heat, rather than convert it, so other measures are needed to describe their thermal performance. The common measures are the coefficient of performance (COP), energy efficiency ratio (EER), and seasonal energy efficiency ratio (SEER). The Efficiency of a Heat pump (HP) and Refrigerators (R)*: 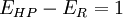If temperatures at both ends of the Heat Pump or Refrigerator are constant and their processes reversible:
Energy efficiency

Annual fuel utilization efficiency (AFUE)
Electrical efficiency
Mechanical efficiency
Figure of merit